

Furthermore, there can be at most one obtuse angle, and a right angle and an obtuse angle cannot occur in the same triangle. Proposition I.17 states that the sum of any two angles in a triangle is less than two right angles, therefore, no triangle can contain more than one right angle. Since triangle D has a right angle, it is a right triangle. An alternate characterization of isosceles triangles, namely that their base angles are equal, is demonstrated in propositions I.5 and I.6.
#Acute isosceles triangle how to#
It is only required that at least two sides be equal in order for a triangle to be isosceles.Įquilateral triangles are constructed in the very first proposition of the Elements, I.1. How to construct (draw) an isosceles triangle with compass and straightedge or ruler, given the length of the base and one side. The way that the term isosceles triangle is used in the Elements does not exclude equilateral triangles. The term isosceles triangle is first used in proposition I.5 and later in Books II and IV. The equilateral triangle A not only has three bilateral symmetries, but also has 120°-rotational symmetries.Īccording to this definition, an equilateral triangle is not to be considered as an isosceles triangle. The scalene triangle C has no symmetries, but the isosceles triangle B has a bilateral symmetry. This definition classifies triangles by their symmetries, while definition 21 classifies them by the kinds of angles they contain. What does an Isosceles Acute Triangle Look Like?Īn isosceles acute triangle looks like an acute triangle with two equal sides and two equal angles less than 90 degrees.Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute. /rebates/2fgremath-help2fisosceles-triangles2ftriangles2fplane-geometry2fgeometry2facute-obtuse-isosceles-triangles&. In this way, we will get an acute isosceles triangle. Now, draw two angles of equal measurements (each should be less than 90 degrees) on both the ends of the line segment. To draw an isosceles acute triangle, the first step is to draw a line segment horizontally which will be the base of the triangle.
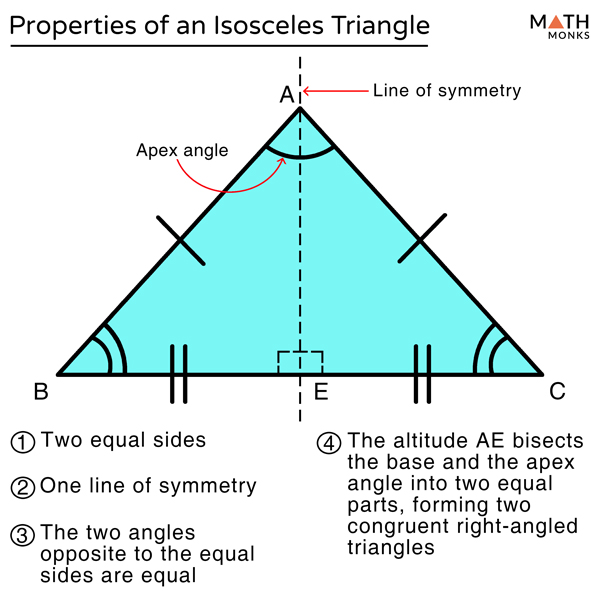
How do you Draw an Acute Isosceles Triangle? Have at least two equal sides and two equal angles.All three angles are acute (less than 90 degrees).The properties of an isosceles acute triangle are listed below: What are the Properties of an Isosceles Acute Triangle? It is usually the unequal side of the isosceles acute triangle. The Isosceles Triangle in which the two legs (equal sides) make an angle less than 90 degrees is called an Isosceles Acute Triangle. The base is the side opposite to the vertex from where the height is drawn or measured. The area of an acute isosceles triangle can be calculated by using the formula: Area = 1/2 × base × height square units. What is the Area of an Isosceles Acute Triangle? At least two of its angles are equal in measurement and all three angles are acute angles.

It comes in the category of both acute triangles and isosceles triangles. So, the perimeter of an isosceles acute triangle = (2a + b) units, where a and b are the sides of the triangle.įAQs on Isosceles Acute Triangle What is an Isosceles Acute Triangle?Īn isosceles acute triangle is a triangle that contains the properties of both the acute triangle and isosceles triangle. To find the isosceles acute triangle perimeter, we just have to add the length of all three sides. Look at the image given below showing isosceles acute triangle formulas for finding area and perimeter.

Where a and b are the sides of the triangle and s is the semi-perimeter, which is (a + a + b)/2 or (2a+b)/2. The two angles opposite the legs are equal and are always acute, so the classification of the triangle as acute, right, or obtuse depends only on the angle.


 0 kommentar(er)
0 kommentar(er)
